原文作者:Mr.Seven
原文地址:八大排序算法总结与java实现
❤查看排序算法动态演示❤查看排序算法动态演示❤查看排序算法动态演示
快速排序 (Quick Sort)
快速排序的名字起的是简单粗暴,因为一听到这个名字你就知道它存在的意义,就是快,而且效率高!
快速排序是一种分而治之思想在排序算法上的典型应用。快速排序是在冒泡排序的基础上进行的改良,快排在面试中也是常客。
基本思想
快速排序的基本思想:挖坑填数+分治法。
先选择一个元素作为基准,通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
动态演示如图,其中第一个基准元素位最后一个元素
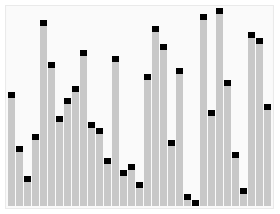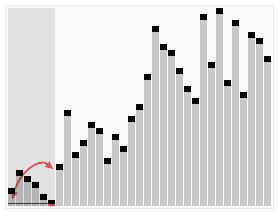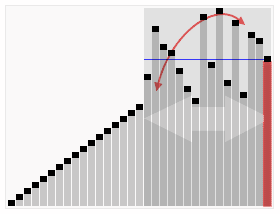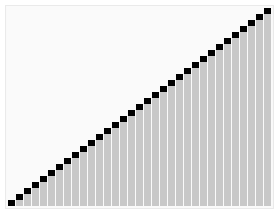
算法描述
快速排序使用分治策略来把一个序列(list)分为两个子序列(sub-lists)。步骤为:
- 从数列中挑出一个元素,称为”基准”(pivot)。
- 重新排序数列,所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准后面(相同的数可以到任一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
- 递归地(recursively)把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归到最底部时,数列的大小是0或1,也就是已经排序好了。这个算法一定会结束,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
如图所示:数组[7,5,6,3,5,1,2,9,5,8,4],以第一个元素7为基准

首次分区后可以得到[5,6,3,5,1,2,4,5]和[7,8,9]两组数据,继续以第一个元素为基准进行两个数组的分区

如此循环往复,即可得到有序序列
Java实现
用伪代码描述如下:
- i = L; j = R; 将基准数挖出形成第一个坑a[i]。(L:左侧下标起点,R:右侧下标起点)
- j–,由后向前找比它小的数,找到后挖出此数填前一个坑a[i]中。
- i++,由前向后找比它大的数,找到后也挖出此数填到前一个坑a[j]中。
- 再重复执行2,3二步,直到i==j,将基准数填入a[i]中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| public class QuickSort {
public static void main(String[] args) {
int[] arr = {49, 38, 65, 97, 26, 13, 27, 49, 55, 4};
System.out.println("排序前:" + Arrays.toString(arr));
int[] a = Arrays.copyOf(arr, arr.length);
quicksort1(a, 0, a.length - 1);
}
private static void quicksort1(int[] arr, int low, int high) {
if (arr.length <= 0 || low >= high) {
return;
}
int leftIndex = low;
int rightIndex = high;
int temp = arr[leftIndex];
while (leftIndex < rightIndex) {
while (leftIndex < rightIndex && arr[rightIndex] >= temp) {
rightIndex--;
}
arr[leftIndex] = arr[rightIndex];
while (leftIndex < rightIndex && arr[leftIndex] <= temp) {
leftIndex++;
}
arr[rightIndex] = arr[leftIndex];
}
arr[leftIndex] = temp;
quicksort1(arr, low, leftIndex - 1);
quicksort1(arr, leftIndex + 1, high);
}
}
|
上面是递归版的快速排序:通过把基准temp插入到合适的位置来实现分治,并递归地对分治后的两个划分继续快排。
那么非递归版的快排如何实现呢?
因为递归的本质是栈,所以我们非递归实现的过程中,可以借助栈来保存中间变量就可以实现非递归了。在这里中间变量也就是通过partition函数划分区间之后分成左右两部分的首尾指针,只需要保存这两部分的首尾指针即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
|
public class QuickSort {
public static void main(String[] args) {
int[] arr = {49, 38, 65, 97, 26, 13, 27, 49, 55, 4};
System.out.println("排序前:" + Arrays.toString(arr));
quickSortByStack(Arrays.copyOf(arr, arr.length));
}
private static void quickSortByStack(int[] arr) {
if (arr.length <= 0) {
return;
}
Stack<Integer> stack = new Stack<Integer>();
stack.push(0);
stack.push(arr.length - 1);
while (!stack.empty()) {
int high = stack.pop();
int low = stack.pop();
int pivot = partition(arr, low, high);
if (pivot > low) {
stack.push(low);
stack.push(pivot - 1);
}
if (pivot < high && pivot >= 0) {
stack.push(pivot + 1);
stack.push(high);
}
}
System.out.println("排序后:" + Arrays.toString(arr));
}
private static int partition(int[] arr, int low, int high) {
if (arr.length <= 0 || low >= high) {
return -1;
}
int leftIndex = low;
int rightIndex = high;
int pivot = arr[leftIndex];
while (leftIndex < rightIndex) {
while (leftIndex < rightIndex && arr[rightIndex] >= pivot) {
rightIndex--;
}
arr[leftIndex] = arr[rightIndex];
while (leftIndex < rightIndex && arr[leftIndex] <= pivot) {
leftIndex++;
}
arr[rightIndex] = arr[leftIndex];
}
arr[leftIndex] = pivot;
return leftIndex;
}
}
|
复杂度
快速排序是通常被认为在同数量级(O(nlog2n))的排序方法中平均性能最好的。
但若初始序列按关键码有序或基本有序时,快排序反而蜕化为冒泡排序。
为改进之,通常以“三者取中法”来选取基准记录,即将排序区间的两个端点与中点三个记录关键码居中的调整为支点记录。快速排序是一个不稳定的排序方法。
| 平均时间复杂度 |
最好情况 |
最坏情况 |
空间复杂度 |
| O(nlog2n) |
O(nlog2n) |
O(n²) |
O(1) |
快速排序排序效率非常高。 虽然它运行最糟糕时将达到O(n²)的时间复杂度, 但通常平均来看, 它的时间复杂为O(nlogn), 比同样为O(nlogn)时间复杂度的归并排序还要快.
适用场景
快速排序似乎更偏爱乱序的数列, 越是乱序的数列, 它相比其他排序而言, 相对效率更高.


