原文作者：Mr.Seven
原文地址：八大排序算法总结与java实现
 ❤查看排序算法动态演示❤查看排序算法动态演示❤查看排序算法动态演示

归并排序 (Merging Sort)

归并排序是建立在归并操作上的一种有效的排序算法。

归并算法用到了分治法的思想,且各层分治递归可以同时进行。(快速排序也引入了分治思想)

基本思想

归并排序算法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

动态示意图如下：
归并排序

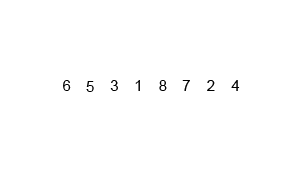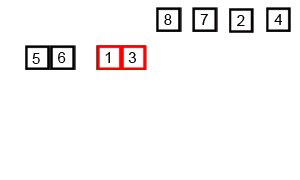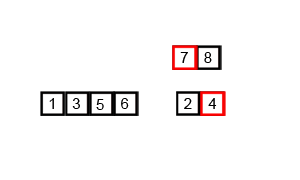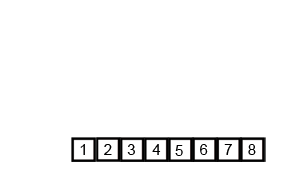
算法描述

归并排序可通过两种方式实现：

自上而下的递归
自下而上的迭代

递归法（假设共有n个元素）

将序列每相邻两个数字进行归并操作，形成floor(n/2)个序列，排序后每个序列包含两个元素
将上述序列再次归并，形成floor(n/4)个序列，每个序列包含四个元素；
重复步骤2，直到所有的元素排序完毕

归并排序

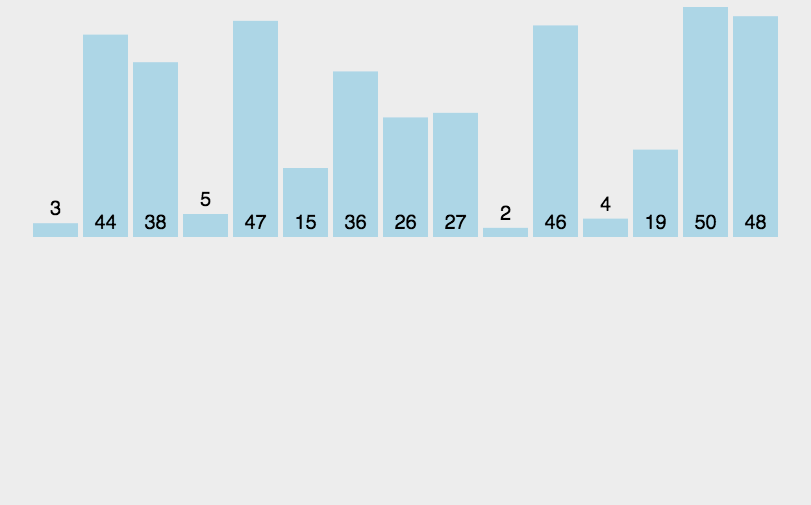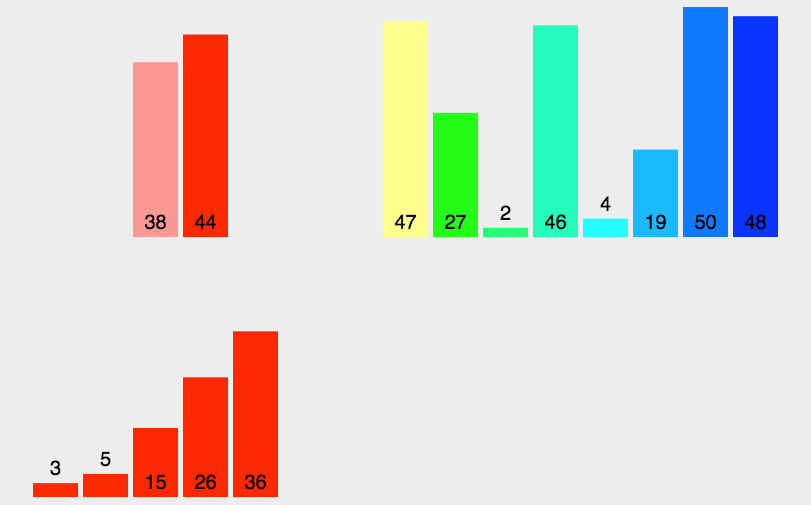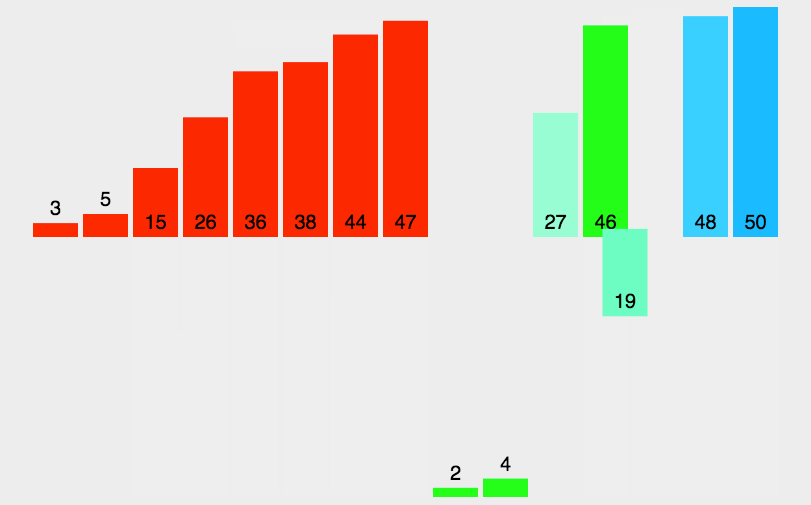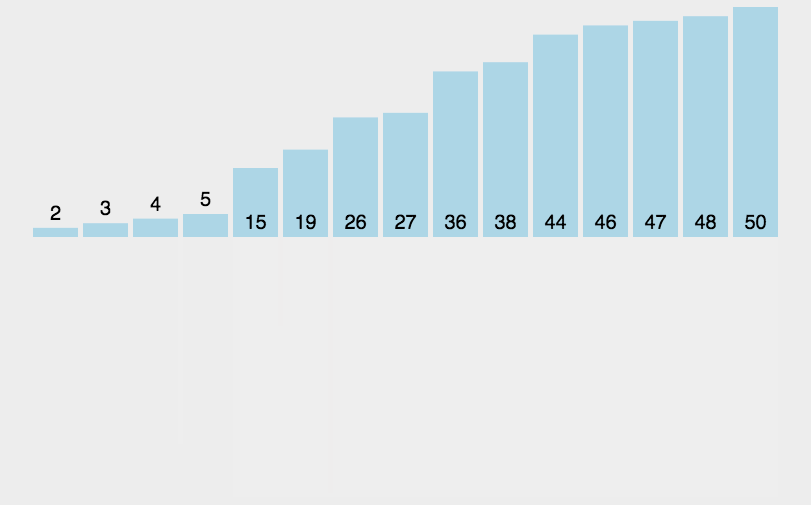
迭代法

申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
设定两个指针，最初位置分别为两个已经排序序列的起始位置
比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
重复步骤③直到某一指针到达序列尾
将另一序列剩下的所有元素直接复制到合并序列尾

Java代码实现

归并排序其实要做两件事：

分解：将序列每次折半拆分
合并：将划分后的序列段两两排序合并

因此，归并排序实际上就是两个操作，拆分+合并

如何合并？

L[first…mid]为第一段，L[mid+1…last]为第二段，并且两端已经有序，现在我们要将两端合成达到L[first…last]并且也有序。

首先依次从第一段与第二段中取出元素比较，将较小的元素赋值给temp[]
重复执行上一步，当某一段赋值结束，则将另一段剩下的元素赋值给temp[]
此时将temp[]中的元素复制给L[]，则得到的L[first…last]有序

如何分解？

在这里，我们采用递归的方法，首先将待排序列分成A,B两组；然后重复对A、B序列分组；直到分组后组内只有一个元素，此时我们认为组内所有元素有序，则分组结束。


/**
 * 描述:
 * 归并排序
 *
 * @author lars
 * @date 2019/9/11 11:46
 */
public class MergingSort {
    public static void main(String[] args) {
        int[] arr = {49, 38, 65, 97, 26, 13, 27, 49, 55, 4};
        System.out.println("排序前:" + Arrays.toString(arr));

        System.out.println(Arrays.toString(mergingSort(Arrays.copyOf(arr,arr.length))));
    }


    private static int[] mergingSort(int[] arr) {

        if (arr.length <= 1) {
            return arr;
        }
        int num = arr.length >> 1;
        int[] leftArr = Arrays.copyOfRange(arr, 0, num);
        int[] rightArr = Arrays.copyOfRange(arr, num, arr.length);

        System.out.println("split two array: " + Arrays.toString(leftArr) + " And " + Arrays.toString(rightArr));
        //递归：将序列拆分为若干个最小单元后进行合并
        return mergeTwoArray(mergingSort(leftArr), mergingSort(rightArr));

    }

    private static int[] mergeTwoArray(int[] arr1, int[] arr2) {
        int i = 0, j = 0, k = 0;

        //申请额外的空间存储合并之后的数组
        int[] result = new int[arr1.length + arr2.length];
        //选取两个序列中的较小值放入新数组
        while (i < arr1.length && j < arr2.length) {
            if (arr1[i] <= arr2[j]) {
                result[k++] = arr1[i++];
            } else {
                result[k++] = arr2[j++];
            }
        }
        //序列1中多余的元素移入新数组
        while (i<arr1.length){
            result[k++]=arr1[i++];
        }
        //序列2中多余的元素移入新数组
        while (j<arr2.length){
            result[k++]=arr2[j++];
        }
//        System.out.println("Merging: " + Arrays.toString(result));
        return result;
    }
}

由上, 长度为n的数组, 最终会调用mergeSort函数2n-1次。通过自上而下的递归实现的归并排序, 将存在堆栈溢出的风险。

复杂度

从效率上看，归并排序可算是排序算法中的”佼佼者”,假设数组长度为n，那么拆分数组共需logn，又每步都是一个普通的合并子数组的过程，时间复杂度为O(n)，故其综合时间复杂度为O(nlogn)。
另一方面，归并排序多次递归过程中拆分的子数组需要保存在内存空间，其空间复杂度为O(n)。

平均时间复杂度	最好情况	最坏情况	空间复杂度
O(nlog2n)	O(nlog2n)	O(nlog2n)	O(n)

交换元素时，可以在相等的情况下做出不移动的限制，所以归并排序是可以稳定的；

和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是O(n log n）的时间复杂度。代价是需要额外的内存空间。

适用场景

若n较大，则应采用时间复杂度为O(nlog2(n))的排序方法：快速排序、堆排序或归并排序

但是如果对算法的稳定性有所要求的话，即相同元素的顺序不被改变，那这时就可以使用归并排序。

因为通过之前文章的分析可以知道快速排序、堆排序都是不稳定的排序算法。