原文作者：Mr.Seven
原文地址：八大排序算法总结与java实现
 ❤查看排序算法动态演示❤查看排序算法动态演示❤查看排序算法动态演示

直接插入排序（Insertion Sort）

插入排序的设计初衷是往有序的数组中快速插入一个新的元素。它的算法思想是：把要排序的数组分为了两个部分, 一部分是数组的全部元素(除去待插入的元素), 另一部分是待插入的元素; 先将第一部分排序完成, 然后再插入这个元素. 其中第一部分的排序也是通过再次拆分为两部分来进行的.

插入排序由于操作不尽相同, 可分为 直接插入排序 , 折半插入排序(又称二分插入排序), 链表插入排序 , 希尔排序 。我们先来看下直接插入排序。

基本思想

将数组中所有元素依次和之前已经排序好的元素序列相比较，如果选择的元素比已排序的元素小，则进行交换，直到所有元素都比较过为止

动态示意图如下:

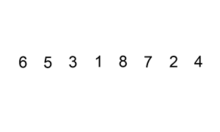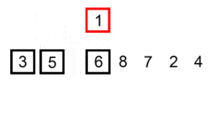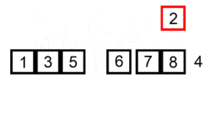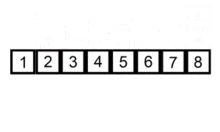
使用插入排序为一列数字进行排序的过程

算法描述

一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：

从第一个元素开始，该元素可以认为已经被排序
取出下一个元素，在已经排序的元素序列中从后向前扫描
如果该元素（已排序）大于新元素，将该元素移到下一位置
重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
将新元素插入到该位置后
重复步骤②~⑤

如下图所示：

直接插入排序

算法实现中比较有意思的一点是，在每次比较操作发现取出来的新元素小于等于已排序的元素时，可以将已排序的元素移到下一位置，
然后将取出来的新元素插入该位置（即相邻位置对调），接着再与前面的已排序的元素进行比较，如上图所示，这样做缺点是交换操作代价比较大。

另一种做法是：将新元素取出（挖坑），从左到右依次与已排序的元素比较，如果已排序的元素大于取出的新元素，那么将该元素移动到下一个位置（填坑），
接着再与前面的已排序的元素比较，直到找到已排序的元素小于等于新元素的位置，这时再将新元素插入进去。就像基本思想中的动图演示的那样。

如果比较操作的代价比交换操作大的话，可以采用二分查找法来减少比较操作的数目。可以认为是插入排序的一个变种，称为二分查找插入排序。

Java代码实现


import java.util.Arrays;

/**
 * 描述:
 * 直接插入排序
 *
 * @author lars
 * @date 2019/9/5 16:30
 */
public class InsertionSort {


    public static void main(String[] args) {
        int[] a = {1, 4, 8, 2, 5};

        insertSort1(a);
        System.out.println(Arrays.toString(a));


        int[] aa = {1, 4, 8, 2, 5};
        insertSort2(aa);
        System.out.println(Arrays.toString(aa));
    }

    /***
     * 交换次数较多实现
     * @param a
     */
    private static void insertSort2(int[] a) {
        for (int i =0 ; i<a.length-1;i++){
            for(int j=i+1;j>0;j--){
                if (a[j-1]>a[j]){
                    //j为待排序元素，j-1为前一位元素，j-1>j交换
                    int temp = a[j];
                    a[j]=a[j-1];
                    a[j-1]=temp;
                }else {
                    //待排序元素大于他前1位元素，位置不变，循环结束
                    break;
                }
            }
        }
    }

    /***
     * 交换次数较少
     * @param a
     */
    private static void insertSort1(int[] a) {
        for (int i = 1; i < a.length; i++) {
            //直接取出第二个元素开始比较，第一个元素默认已完成排序
            int temp = a[i];
            // temp与他前面的有序元素依次比较，找到自己的位置
            for (int j = i; j >= 0; j--) {
                //temp小于他前一位的元素，交换位置，
                // 继续循环比较(j>0如果不成立，说明已经比较到0位置,说明temp属于当前最小，直接放当前位置)
                if (j > 0 && a[j - 1] > temp) {
                    a[j] = a[j - 1];
                    //相互交换（可以先不进行移动）
                    //a[j-1] = temp;
                } else {
                    //temp大于他前面的元素，temp就放置在当前位置
                    a[j] = temp;
                    //该元素位置确定，结束循环，到下一个
                    break;
                }
            }
        }

    }

}

复杂度

直接插入排序复杂度如下：

最好情况下，排序前对象已经按照要求的有序。比较次数(KCN)：n−1；移动次数(RMN)为0。则对应的时间复杂度为O(n)。
最坏情况下，排序前对象为要求的顺序的反序。第i趟时第i个对象必须与前面i个对象都做排序码比较，并且每做1次比较就要做1次数据移动（从上面给出的代码中看出）。比较次数(KCN)：n²/2 ; 移动次数(RMN)为：n²/2。则对应的时间复杂度为O(n²)。
如果排序记录是随机的，那么根据概率相同的原则，在平均情况下的排序码比较次数和对象移动次数约为n²/2，因此，直接插入排序的平均时间复杂度为O(n²)。

平均时间复杂度	最好情况	最坏情况	空间复杂度
O(n²)	O(n)	O(n²)	O(1)

Tips: 由于直接插入排序每次只移动一个元素的位，并不会改变值相同的元素之间的排序，因此它是一种稳定排序。