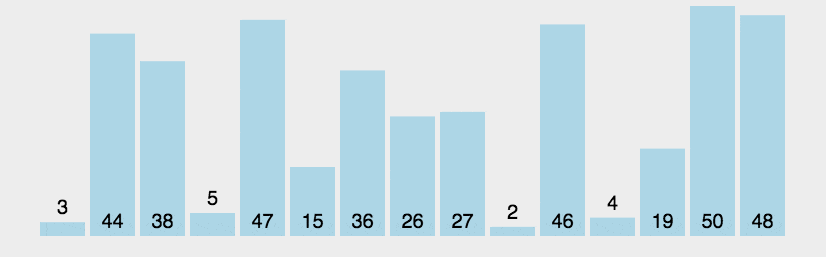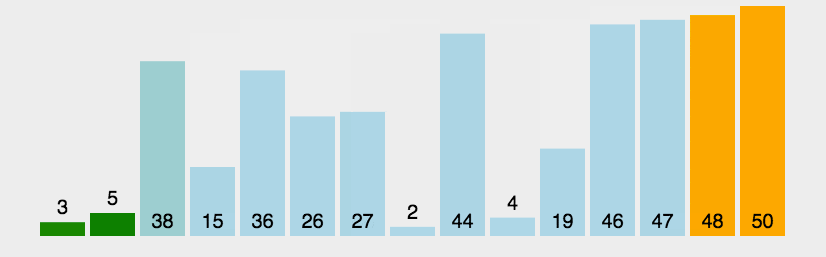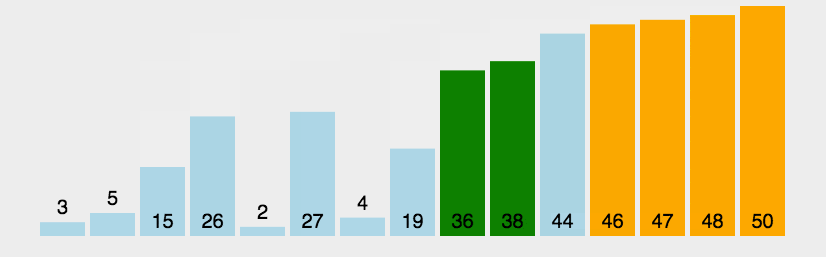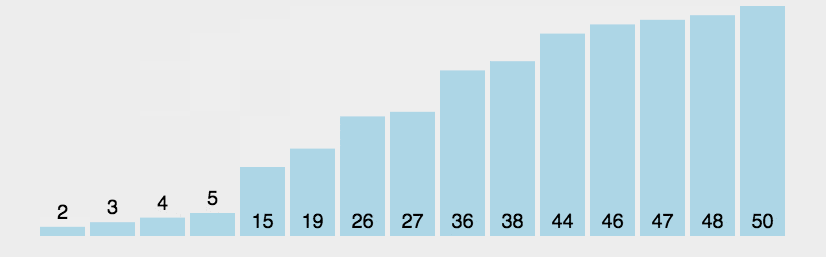本文参考于:八大排序算法总结与java实现
❤查看排序算法动态演示❤查看排序算法动态演示❤查看排序算法动态演示
冒泡排序 (Bubble Sort)
冒泡应该是大部分同学第一个接触到的排序算法,冒泡在面试中也有很高的出现频率。所以务必要将其掌握。
基本思想
冒泡排序依次遍历要排序的元素序列,依次比较两个相邻的元素,如果他们的顺序错误就进行交换。如此往复,知道待排序列中没有相邻元素要交换时排序完成。
其动态演示如图:
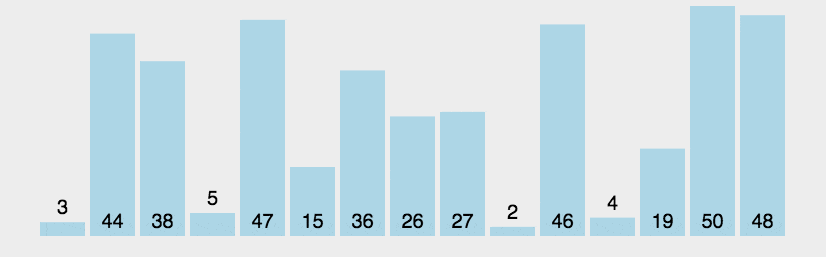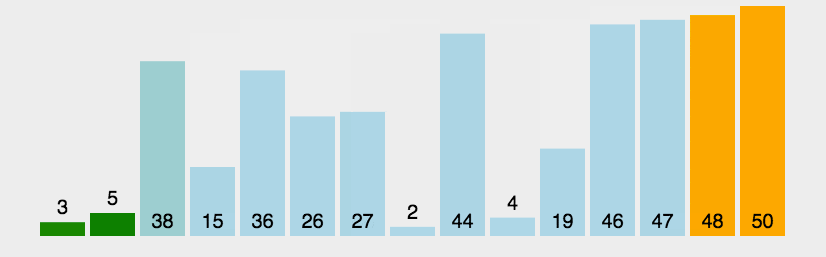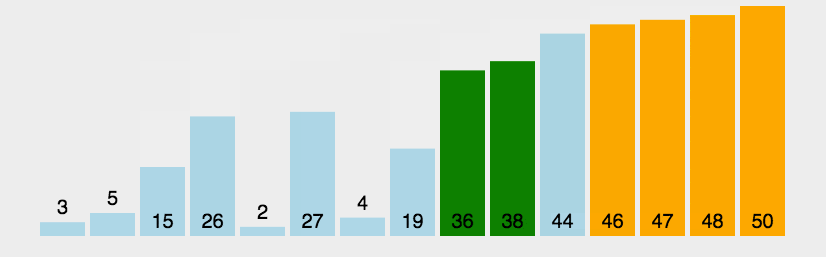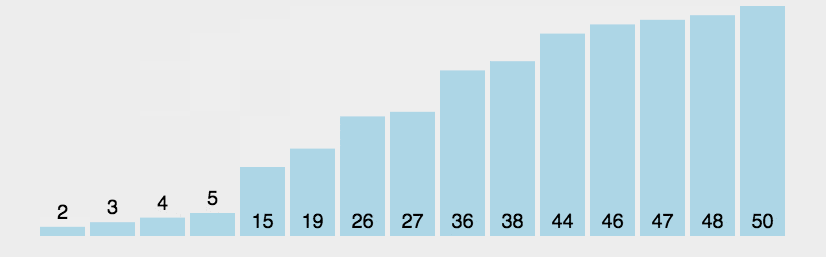
从其动态图可以看出,冒泡排序法在每轮遍历后都会将最大或者最小的元素慢慢的浮到顶端,这种下现象就像气泡上浮一般,所以算法命名冒泡排序
算法描述
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
JAVA实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
public class BubbleSort {
public static void main(String[] args) {
int[] arr = {49, 38, 65, 97, 26, 13, 27, 49, 55, 4};
System.out.println("排序前:" + Arrays.toString(arr));
Bubble(Arrays.copyOf(arr, arr.length));
}
private static void Bubble(int[] arr) {
for (int i = 1; i < arr.length; i++) {
for (int j = 0; j < arr.length - i; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
System.out.println("排序后:" + Arrays.toString(arr));
}
}
|
冒泡排序还有一种优化算法,就是建立一个 flag,当在一趟序列遍历中元素没有发生交换,则证明该序列已经有序,即可结束遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
private static void BubbleDemo(int[] arr) {
for (int i = 1; i < arr.length; i++) {
boolean flag = true;
for (int j = 0; j < arr.length - i; j++) {
if (arr[j] > arr[j + 1]) {
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
flag = false;
}
}
if (flag) {
break;
}
}
}
|
复杂度
- 最好情况:序列原本有序(一轮遍历)时间复杂度为O(n)
- 最差情况:序列为反序,时间复杂度为O(n²)
平均来讲, 时间复杂度为O(n²),
冒泡排序中只有缓存的temp变量需要内存空间, 因此空间复杂度为常量O(1).
Tips: 由于冒泡排序只在相邻元素大小不符合要求时才调换他们的位置, 它并不改变相同元素之间的相对顺序, 因此它是稳定的排序算法.
| 平均时间复杂度 |
最好情况 |
最坏情况 |
空间复杂度 |
| O(n²) |
O(n) |
O(n²) |
O(1) |
适用场景
主要看数据的顺序情况,如果数据本身已经是离最终排序结果不远的,通过加个交换标识,冒泡排序可能是更快的。
所以所有排序算法的试用性都是分场景来看的,但是不得不承认冒泡排序在性能要求高的场景下,通用性不高